数学与二进制

抛出问题

0.1 + 0.2 === 0.3 -----> false 为啥?😒

框架、轮子源码里的位运算到底啥意思?

// React源码
function clz32Fallback(x: number): number {
  const asUint = x >>> 0;
  if (asUint === 0) {
    return 32;
  }
  return (31 - ((log(asUint) / LN2) | 0)) | 0;
}

// Vue源码
function repeat(str: string, n: number) {
  let result = ''
  if (n > 0) {
    // eslint-disable-next-line no-constant-condition
    while (true) {
      // eslint-disable-line
      if (n & 1) result += str
      n >>>= 1
      if (n <= 0) break
      str += str
    }
  }
  return result
}

以上两个问题如果知道答案, 请略过本文

数学公式与推导

任何一个数学公式都可以用图形表示

完全平方公式

(a + b)² = (a + b) x (a + b) = a² + 2ab + b²

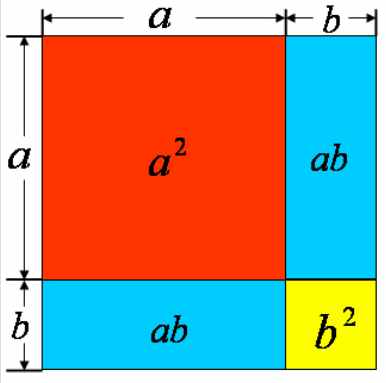
(a - b)² = (a - b) x (a - b) = a² - 2ab + b²

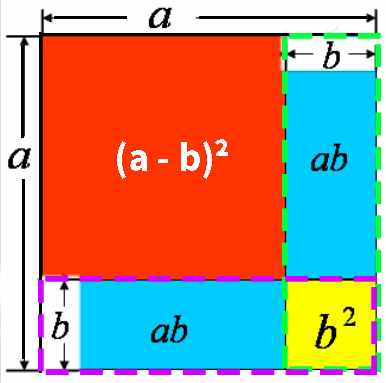
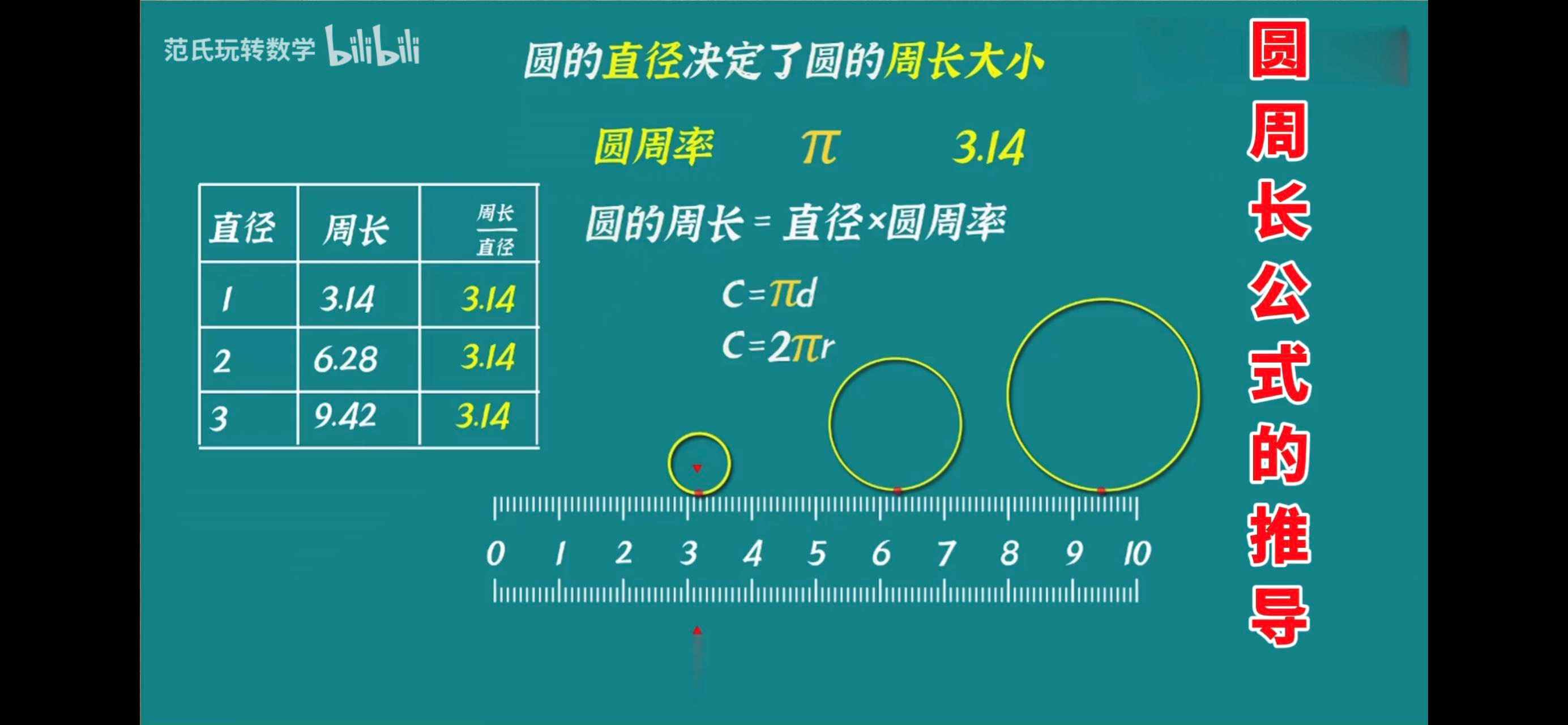
圆周长公式

C = 2 x π x r

三角形面积

这个10x10图形真是存在
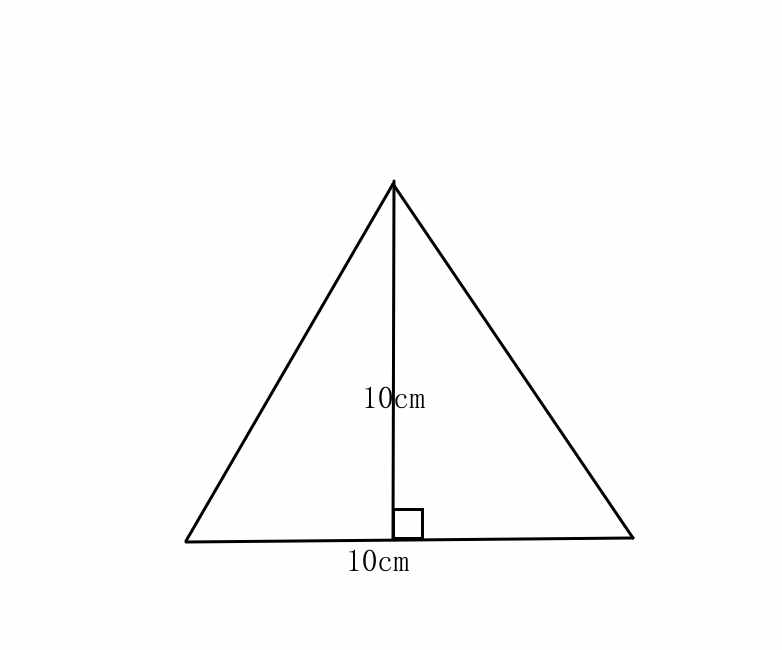
这个5x6的等腰直角三角形并不存在
所以大家思考问题的时候, 如果从原理入手, 不仅能理解问题、解决问题、还能避免问题
原因如下:

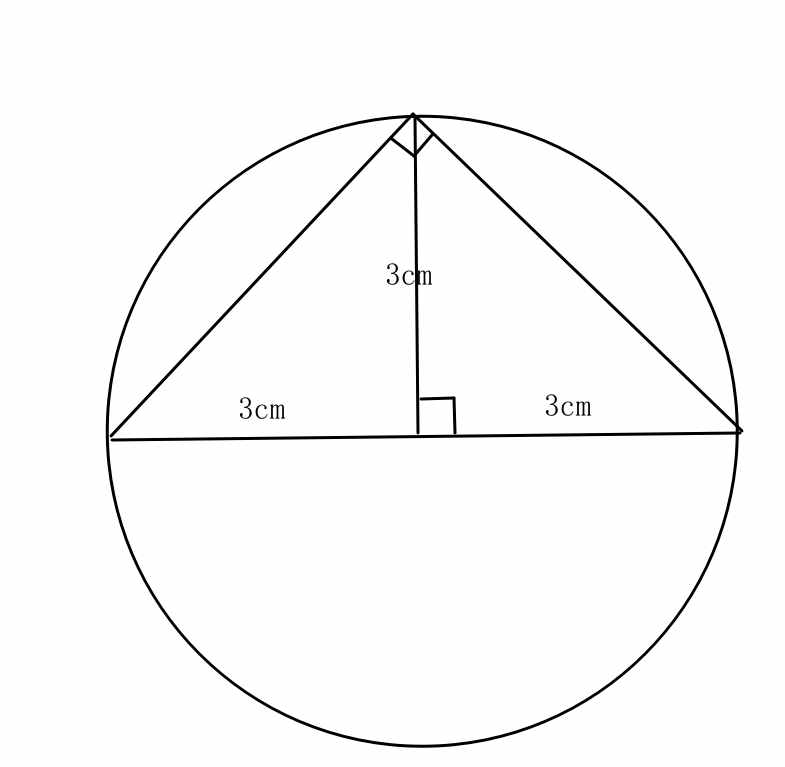
二进制与四则运算

二进制与十进制的取舍

比分牌其实就是十进制的物理体现

十进制转二进制

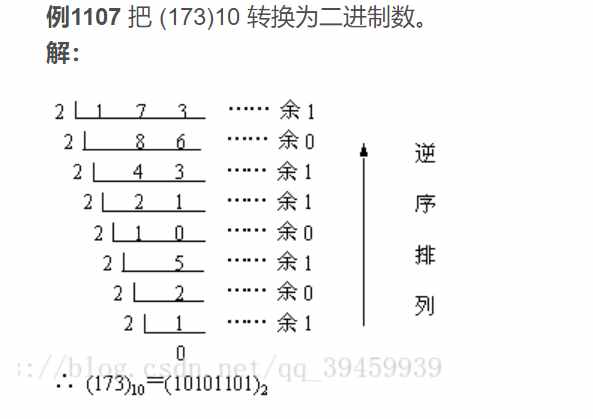
原码(true form)

是一种计算机中对数字的二进制定点表示方法。

原码表示法在数值前面增加了一位符号位（即最高位为符号位）：正数该位为0，负数该位为1（0有两种表示：+0和-0），其余位表示数值的大小。

正负数表示

一个正数，按照绝对值大小转换成的二进制数就是正数的原码一个负数，按照绝对值大小转换成的二进制数，然后最高位补1，就是负数的原码
比如
00000000 00000000 00000000 00000101 是5的原码。
10000000 00000000 00000000 00000101 是-5的原码。

计算数学加法: 1 + 1 = 2

00000000 00000000 00000000 00000001   ->   1
+
00000000 00000000 00000000 00000001   ->   1
=
00000000 00000000 00000000 00000010   ->   2

加法器

四则运算的【减/乘/除】只是变相的【加法】而已

与非门进位

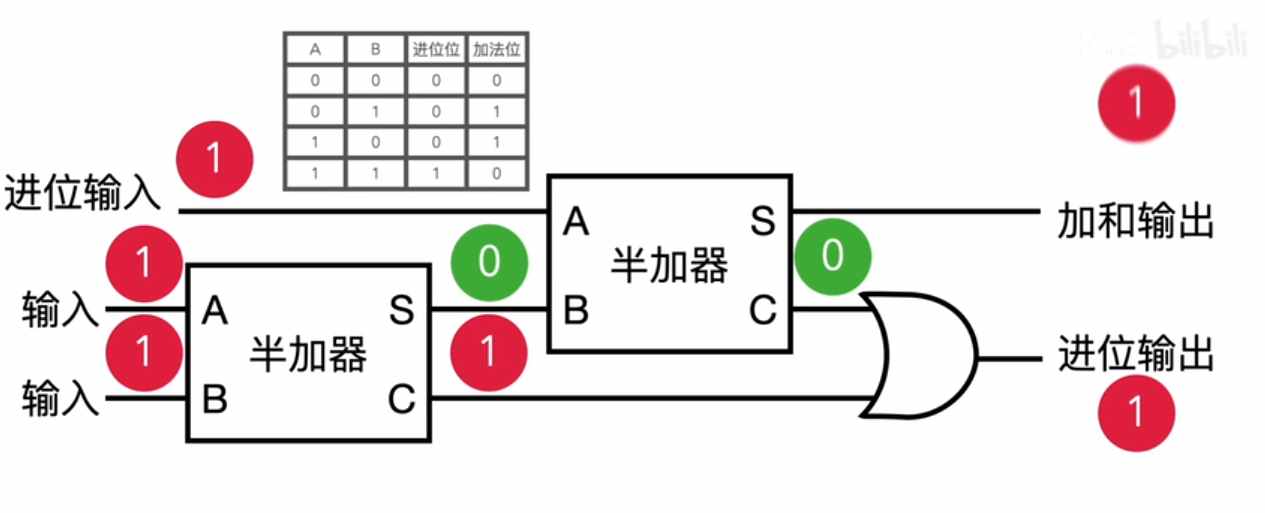
二进制乘法

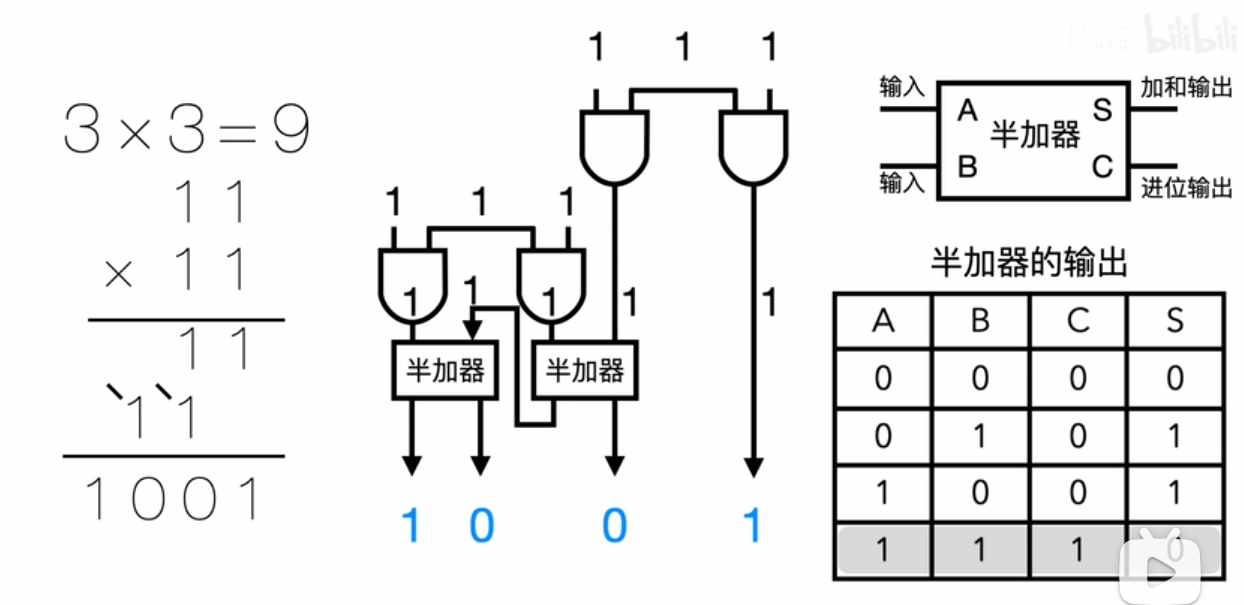
计算数学减法: 1 + (-1) = -2

00000000 00000000 00000000 00000001   ->   1
+
10000000 00000000 00000000 00000001   ->  -1
=
10000000 00000000 00000000 00000010   ->  -2

结果不为0显然直接用【原码】参与运算就会出现这么尴尬的问题
这也是【反码】【补码】出现的一部分原因,

具象的钟表

10 % 2 取模+- 取余+
就像钟表1点走到3点: '顺时针走了2个刻度【+2】' === '逆时针走了10个刻度【-10】'; 换成代码:

1+(-2)  =  11
0+0+0+0+0+1+(0-2)  =11



1+(12-2)


// 初始时间
const originTime = 1;
// 当前时间
const currentTime = 3;
// 时制
const timeSystem = 12;
// 【正数】的运算
console.log(currentTime === originTime + (+2));
// 3 === 1 + 2
// true

// 【负数】的运算
// 加timeSystem可以理解为时钟多转了一圈,【-10】=【实际走的刻度数(顺时针偏移量)】-【时制】
console.log(currentTime === originTime + (-10) + timeSystem);
// 3 === 1 - 10 + 12
// true
// 这个甚至可以推广为公式【时间逆时针差值】=【当前时间-初始时间】=【实际走的刻度数(顺时针偏移量)】-【时制】

1-2



0110 原码
1001 反码
1010 补码

000

1101
0010
0011

反码与补码

计算机二进制码通过补码快速表示

二进制补码转十进制

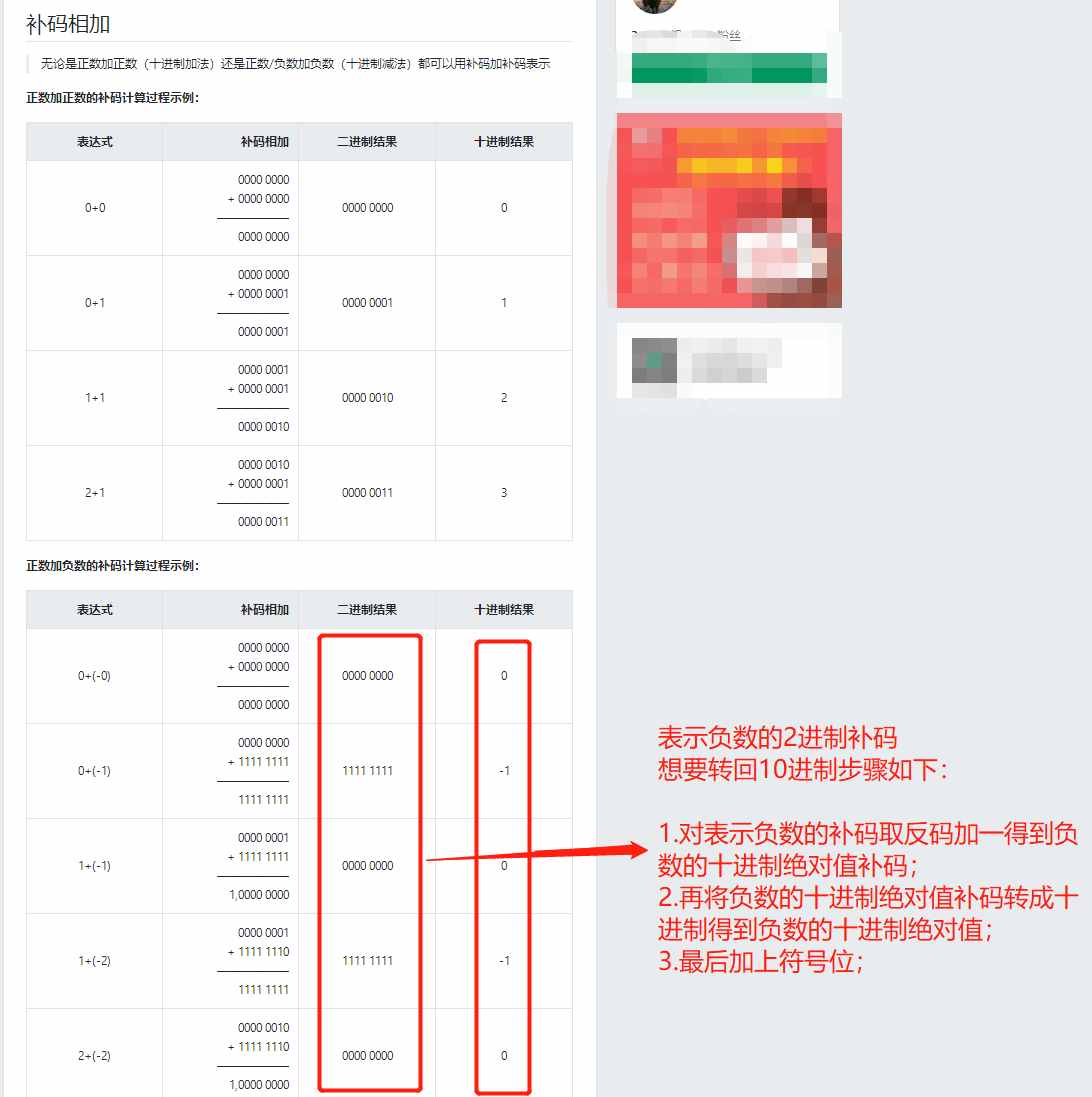
二进制与小数

整数与分数

$$ \frac{5}{1} = 5 $$
$$ \frac{99}{1} = 99 $$

倒数

设一个数x与其相乘的积为1的数，记为1/x，
意思是除了0以外的数都存在倒数，分子和分母相倒并且两个乘积是1的数互为倒数，0没有倒数

$$ 1 \div \frac{99}{1} = \frac{1}{99} $$

负次方

一个数的负次方即为这个数的正次方的倒数
2 ^ -1

$$ 99^{-1} = \frac{1}{99} $$

小数的十进制转二进制

0.5      -> 1/2 ->  2^-1 -> 00000000 00000000 . 10000000 00000000
0.25     -> 1/4 ->  2^-2 -> 00000000 00000000 . 01000000 00000000
0.125    -> 1/8 ->  2^-3 -> 00000000 00000000 . 00100000 00000000
0.0625   -> 1/16 -> 2^-4 -> 00000000 00000000 . 00010000 00000000
0.03125  -> 1/32 -> 2^-5 -> 00000000 00000000 . 00001000 00000000
......

0.75  -> 
0.5 + 0.25 -> 
1/2 + 1/4 -> 
2^-1  + 2^-2 ->
00000000 00000000 . 11000000 00000000

把二进制数110.11转换成十进制数。

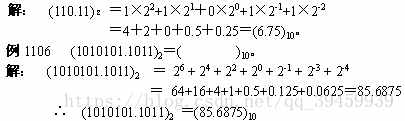
精度标准

前端位运算

https://www.jianshu.com/p/eaba50c3d824

位运算实际使用场景

判断小数和相等
- console.log(0.1 + 0.2 === 0.3)
- 0.1 + 0.2 === 0.3000000000000000(2-7)
- 解决办法: 0.1*10+ 0.2 * 10 = 3
- 如果结果不要求特别精确，可以先计算，再将最终结果保留小数，注意计算过程中最好不要取舍，最后的结果再保留小数。
vue和react中的位运算
- https://zhuanlan.zhihu.com/p/148441522
前端位运算场景
- https://blog.csdn.net/u010651383/article/details/104556393
位运算的缺点 > 被eslint禁用 https://eslint.bootcss.com/docs/rules/no-bitwise

三进制-最高效的进制

现今的计算机都使用“二进制”数字系统，尽管它的计算规则非常简单，但其实“二进制”逻辑并不能完美地表达人类的真实想法。相比之下，“三进制”逻辑更接近人类大脑的思维方式。因为在一般情况下，我们对问题的看法不是只有“真”和“假”两种答案，还有一种“不知道”。在三进制逻辑学中，符号“1”代表“真”；符号“-1”代表“假”；符号“0”代表“不知道”。显然，这种逻辑表达方式更符合计算机在人工智能方面的发展趋势。它为计算机的模糊运算和自主学习提供了可能。只可惜，电子工程师对这种非二进制的研究大都停留在表面或形式上，没有真正深入到实际应用中去。
“Сетунь”小型数字计算机的设计计划由科学院院士С·Л·Соболев在1956年发起。这个计划的目的是为大专院校、科研院所、设计单位和生产车间提供一种价廉物美的计算机。为此，他在莫大计算机中心成立了一个研究小组。该小组最初由9位年轻人（4名副博士、5名学士）组成，都是工程师和程序员。С·Л·Соболев、К·А·Семендяев、М·Р·Шура-Бура和И·С·Березин是这个小组的永久成员。他们经常在一起讨论计算机架构的最优化问题以及如何依靠现有的技术去实现它。他们甚至还设想了一些未来计算机的发展思路。
随着技术的进步，真空管和晶体管等传统的计算机元器件逐渐被淘汰，取而代之的是速度更快、可靠性更好的铁氧体磁芯和半导体二极管。这些电子元器件组成了一个很好的可控电流变压器，这为三进制逻辑电路的实现提供了可能，因为电压存在着三种状态：正电压（“1”）、零电压（“0”）和负电压（“-1”）。三进制逻辑电路非但比二进制逻辑电路速度更快、可靠性更高，而且需要的设备和电能也更少。这些原因促成了三进制计算机“Сетунь”的诞生。
三进制代码的一个特点是对称，即相反数的一致性，因此它就和二进制代码不同，不存在“无符号数”的概念。这样，三进制计算机的架构也要简单、稳定、经济得多。其指令系统也更便于阅读，而且非常高效。
在这群天才青年日以继夜的开发和研制下，“Сетунь”的样机于1958年12月准备完毕。在头两年测试期，“Сетунь”几乎不需要任何调试就运行得非常顺利，它甚至能执行一些现有的程序。1960年，“Сетунь”开始公共测试。
1960年4月，“Сетунь”就顺利地通过了公测。它在不同的室温下都表现出惊人的可靠性和稳定性。它的生产和维护也比同期其它计算机要容易得多，而且应用面广，因此“Сетунь”被建议立即投入批量生产。
不幸的是，苏联官僚对这个不属于经济计划一部分的“科幻产物”持否定的态度。他们甚至勒令其停产。而此时，对“Сетунь”的订单却如雪片般从各方飞来，包括来自国外的订单，但10到15台的年产量远不足以应付市场需求，更不用说出口了。很快，计划合作生产“Сетунь”的捷克斯洛伐克工厂倒闭了。1965年，“Сетунь”停产了。取而代之的是一种二进制计算机，但价格却贵出2.5倍。
“Сетунь”总共生产了50台（包括样机）。30台被安装在高等院校，其余的则在科研院所和生产车间落户。从加里宁格勒到雅库茨克，从阿什哈巴德到新西伯利亚，全苏都能看到“Сетунь”的身影。各地都对“Сетунь”的反应不错，认为它编程简单（不需要使用汇编语言），支持反向波兰表示法，适用于工程计算、工业控制、计算机教学等各个领域。